Antje Völkel, Technician

AUC Service for internal and external users

Analytical Ultracentrifugation (AUC) is a powerful fractionating analysis method for colloids and polymers. Traditionally, it is used as absolute technique for molar mass determination and interaction analysis of biopolymers. Since AUC is capable to analyze all dispersed systems from solutions and dispersions via liquid crystals to gels, it is a universal technique for colloid and polymer science. Therefore, this technique still has a huge development potential for new analysis methods – even more than 80 years after the introduction of the technique. AUC is available as an active service unit for a large variety of colloid and polymer analysis problems from the institute and external cooperation partners. We have three main working directions in this project: a) detector development b) method development c) colloid and polymer characterization as service measurements. It is impossible to give an overview of the work but the examples below shall give an impression what is possible in the AUC analytical service.

AUC is a versatile analytical technique, which can be applied to many more analytical questions than the traditional molar mass or sedimentation coefficient distribution. For the example of microgels containing partially uncrosslinked material, the amount of each component can be quantitatively determined. However, the sedimentation coefficients depend on the friction so that a sedimenting swollen microgel has a higher friction and thus lower sedimentation coefficient compared to the unswollen microgel. Therefore, the swelling degree can be calculated from the sedimentation coefficients of swollen and non-swollen samples. Determining the sedimentation coefficient distribution of swollen and deswollen microgels for the first time enabled the determination of a swelling degree distribution as shown in Fig. 1. Despite some instability of the evaluation at the highest swelling degree of the weakly crosslinked microgel, the swelling degree distributions allow for a detailed analysis of the homogeneity of crosslinking, which is expressed in a narrow swelling degree distribution.

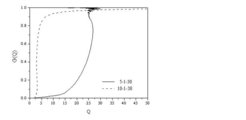
Fig. 1: Integral volume degree of swelling distributions evaluated from sedimentation coefficient distributions in the collapsed and swollen state for a highly crosslinked (10-1-30) and weakly crosslinked (5-1-30) microgel of poly(N-isopropylacrylamide) (NIPAAm).

Fig. 1: Integral volume degree of swelling distributions evaluated from sedimentation coefficient distributions in the collapsed and swollen state for a highly crosslinked (10-1-30) and weakly crosslinked (5-1-30) microgel of poly(N-isopropylacrylamide) (NIPAAm).

However, in the present example, it can be seen that the highly crosslinked microgel (10-1-30) has a tailing towards higher swelling degrees meaning that ca. 5 % of the microgels are more weakly crosslinked. In turn, the weakly crosslinked microgel has a similar fraction of more crosslinked microgels.

If hybrid colloids or very small colloids are investigated by AUC, the determination of the particle density is often problematic, as the samples can exhibit a density distribution. This could in principle be accessed by density gradient ultracentrifugation for densities up to 2 g/ml. However, particle stability issues hinder the application of salts and organic solvent mixtures endanger preferential solvation problems. Application of the density variation method running experiments in H2O and D2O combining the respective sedimentation coefficient distributions can circumvent this problem and can yield density distributions with a quite robust determination of the particle density. This method appears promising for the analysis of hybrid organic-inorganic as well as nanoparticles with higher density by AUC.

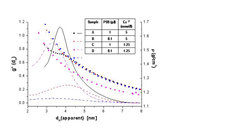
Fig. 2: Apparent particle size and density distribution of amorphous calcium carbonate precursor particles from the density variation method for samples with different CaCO3/poly(syrene sulfonate) ratios — Fig. 2: Apparent particle size and density distribution of amorphous calcium carbonate precursor particles from the density variation method for samples with different CaCO₃/poly(syrene sulfonate) ratios

Fig. 2: Apparent particle size and density distribution of amorphous calcium carbonate precursor particles from the density variation method for samples with different CaCO₃/poly(syrene sulfonate) ratios

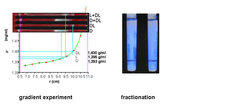
Density gradient ultracentrifugation can be applied to separate racemate crystals from excess enantiomer crystals. Although density gradient techniques have been well-established for decades to separate various biopolymers from mixtures or biopolymers with subtle density differences like single- and double-stranded DNA, they have not been applied to the separation of chiral compounds. Solid racemic compounds differ significantly in density from the corresponding pure enantiomers. This difference can be as large as 5%. On average, the racemic compounds in the solid state are denser than the corresponding enantiomers (Wallach’s rule). Therefore, the application of density gradient ultracentrifugation is well-suited to separate excess enantiomers from racemates with a high accuracy of the third digit in density and good recovery rates between 75 and 90%.

Fig. 3: Separation of DL-alanin crystals from the pure enantiomer crystals by density gradient ultracentrifugation in a Nycodenz gradient. The left figure (upper) shows the bands in the ultracentrifuge tubes and the lower part shows the corresponding calibration curve which allows the determination of the sample density. The right figure shows the separation of L- resp. D-alanin (upper band at meniscus) from the denser racemate (lower band) with a Nycodenz solution with intermediate density

Fig. 3: Separation of DL-alanin crystals from the pure enantiomer crystals by density gradient ultracentrifugation in a Nycodenz gradient. The left figure (upper) shows the bands in the ultracentrifuge tubes and the lower part shows the corresponding calibration curve which allows the determination of the sample density. The right figure shows the separation of L- resp. D-alanin (upper band at meniscus) from the denser racemate (lower band) with a Nycodenz solution with intermediate density

We have developed the methodology to characterize the osmotic pressure of solutions or swelling pressure of gels by AUC further, to include the determination of the equation of state of liquid crystalline systems via osmotic pressure measurements in sedimentation equilibrium. These measurements include the determination of phase boundaries, which are very difficult to obtain otherwise. For laponite clay dispersions, it could be demonstrated that a continuous dependence of the osmotic pressure, over orders of magnitude between at least ~101 and 104 Pa, and a wide concentration range, can be determined in agreement with standard theoretical considerations in one experiment. Two regimes - counter-ion ideal gas and interacting double layers - can be easily identified in the equation of state, whereas metastable glass- or microphase-separated gel states previously encountered in osmotic stress measurements of laponite are circumvented. Fig. 3 shows the good agreement of the measured osmotic pressures with those derived from theoretical models for the dilute and concentrated regime. These results show the advantage of the AUC experiment, which yields hundreds of osmotic pressure concentration pairs over the traditional time consuming osmotic stress approach which yields only a single data pair. Also the possibility to investigate multiphase systems and phase boundaries in a single experiment demonstrates the power of the approach.

Fig. 4: Osmotic pressure (log scale) plotted against water layer thickness, lw for disc-like laponite RD particles of thickness 1 nm and diameter 25 nm. Open squares: AUC experimental data; open circles: literature experimental data from osmotic stress experiments. Solid line in the high and low concentration regime: theoretical osmotic pressure. Vertical lines delineate the literature-determined phase boundaries at lw = 67 and 230 nm, and the Debye length for 10–3 M salt, of ~10 nm. Inset: The experimental data in the low-concentration regime, and the calculated osmotic pressure for average particle diameters of 20 nm (solid black line), 25 nm (grey line) and 30 nm (dashed black line), shown on a linear scale. — Fig. 4: Osmotic pressure (log scale) plotted against water layer thickness, lw for disc-like laponite RD particles of thickness 1 nm and diameter 25 nm. Open squares: AUC experimental data; open circles: literature experimental data from osmotic stress experiments. Solid line in the high and low concentration regime: theoretical osmotic pressure. Vertical lines delineate the literature-determined phase boundaries at lw = 67 and 230 nm, and the Debye length for 10^–3M salt, of ~10 nm. Inset: The experimental data in the low-concentration regime, and the calculated osmotic pressure for average particle diameters of 20 nm (solid black line), 25 nm (grey line) and 30 nm (dashed black line), shown on a linear scale.

Fig. 4: Osmotic pressure (log scale) plotted against water layer thickness, lw for disc-like laponite RD particles of thickness 1 nm and diameter 25 nm. Open squares: AUC experimental data; open circles: literature experimental data from osmotic stress experiments. Solid line in the high and low concentration regime: theoretical osmotic pressure. Vertical lines delineate the literature-determined phase boundaries at lw = 67 and 230 nm, and the Debye length for 10^–3M salt, of ~10 nm. Inset: The experimental data in the low-concentration regime, and the calculated osmotic pressure for average particle diameters of 20 nm (solid black line), 25 nm (grey line) and 30 nm (dashed black line), shown on a linear scale.

Gelatin is an example of a polymer with polydispersity is size and structure. Depending on the production process (and the raw material) gelatin consists of proteins, peptides and oligomers in chains of different molecular weights in the range between 10 and 300 kDa. Gelatin forms helices and theses helices aggregate in solution. Thus, molecules with different axial ratios and thus different frictional ratios are expected. With two dimensional spectrum analysis (2DSA) such a heterogenity can be resolved.

*Fig. 5: 2DSA-Mc pseudo 3d plots of 3; 5 and 10 mg/ml gelatin in 0.5 M NaCl. Measurement was performed at 60000 rpm with an Rayleigh interference optics.*

*Fig. 5: 2DSA-Mc pseudo 3d plots of 3; 5 and 10 mg/ml gelatin in 0.5 M NaCl. Measurement was performed at 60000 rpm with an Rayleigh interference optics.*

With increasing concentration a slower sedimentation is observed. On the other hand, the frictional coefficient (f/f0) is increasing because of aggregation of gelatin and thus extension in the length of the molecule. Calculations were performed on the UltraScan LIMS cluster (http://uslims.uthscsa.edu/mpig/) at the Bioinformatics Core Facility at the University of Texas Health Science Center at San Antonio and the Lonestar cluster at the Texas Advanced Computing Center supported by NSF Teragrid Grant #MCB070038 (to Borries Demeler) using the ULTRASCAN software (http://www.ultrascan.uthscsa.edu/).