Biomimetic Actuation and Tissue Growth

Biomimetic Actuation and Tissue Growth

Natural materials may change their shape and structure throughout their lifetime. Examples range from the development of organs during embryogenesis, the healing of damaged tissues, to passive humidity driven plant motion. Such examples are driven either through the formation of new tissue in particular locations or via the heterogeneous deformation of already existing tissues. The resultant macroscopic shape change is then controlled by geometry - the geometry of the constraining environment and the geometry of how the deforming tissues are arranged inside the material itself. In this group we investigate this general theme with a focus on two main directions using both theoretical and experimental techniques:

  1. The materials design of natural and biomimetic actuators
  2. The effect of geometry on collective cell behaviour or tissue growth

Biomimetic Actuation

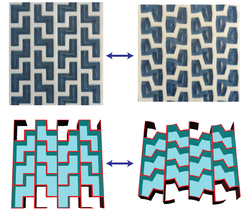
Swelling of porous actuators can be controlled by cell-geometry (above, swelling of 3D printed honeycombs, below, finite element simulations of the same structures). For more information see Guiducci et al 2015.

Our inspiration comes from plant systems (See also the group of Michaela Eder), which can show complex motion through the passive absorption of water, for example in the pine cone and wheat awns. These systems are particularly interesting in that the organs are both structure and motor in one, the motion being controlled by the geometric arrangement of constituent tissues with different swellabilities. Our main focus is here is to firstly develop mechanical models for simple biomimetic systems, and to apply these to natural plant systems. Furthermore, we are interested in exploring the design space of actuation driven by material architecture. We then aim to apply the design principles learnt to new biomimetic composites and create prototypes using advanced 3D printing technology.

Related References:

  • Harrington, M. J., et al. (2011). Origami-like unfolding of hydro-actuated ice plant seed capsules. Nature Communications, 2, 337–7.
  • Stoychev, G., et al. (2012). Shape-Programmed Folding of Stimuli-Responsive Polymer Bilayers. ACS Nano, 6, 3925-2934.
  • Stoychev, G., et al. (2013) Hierarchical multi-step folding of polymer bilayers, Advanced Functional Materials, 23, 2295-2300
  • Guiducci, L., et al. (2014) Pressurized honeycomb as soft-actuators: a theoretical study, Journal of the Royal Society Interface, 11: 20140458.
  • Razghandi, K., et al. (2014) Hydro-actuation of ice plant seed capsules powered by water uptake, Bioinspired, Biomimetic and Nanobiomaterials 3, 169-182.
  • Zhao, Q., et al. (2014) An instant multi-responsive porous polymer actuator operating via solvent molecule sorption, Nature Communications, 5, 4293.
  • Zhao, Q., et al. (2015) Porous poly(ionic liquid) actuator with ultra-high sensitivity to solvents, Advanced Materials 27, 2913-2917.
  • Guiducci, L., et al. (2015) The Geometric Design and Fabrication of Actuating Cellular Structures, Advanced Materials Interfaces, 2, 1500011.
  • Stoychev, G., et al. (2016) Hole-programmed superfast multistep actuation of polymer bilayers, Advanced Functional Materials, , 26, 7733-7739.
  • Gong, J., et al. (2017) Hierarchically arranged helical fiber actuators derived from commercial cloth, Advanced Materials DOI: 10.1002/adma.201605103
Simulated tissue formation by pre-osteoblast cells in square- and cross-shaped pores (left) compared with in-vitro tissue growth (middle). Actin (green) and nuclei (red) staining highlight the role of pore geometry on the internal tissue structure. For more information see Bidan et al, 2013

Tissue Growth

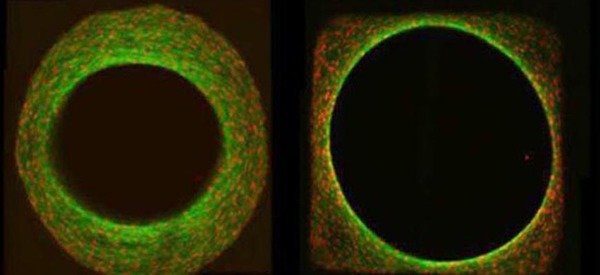
In addition to being controlled by biochemical factors, tissue growth is also effected by the physical properties of the local cell environment such as stiffness and shape. We are particularly interested in evidence that the local geometry, namely the surface curvature of the substrate, controls the rate of cell proliferation and resultant tissue growth. Our goal is to combine theoretical models for tissue growth with in-vitro cell-culture experiments in order to understand the observed dependence of growth behaviour on curvature. We then aim to use our models to better understand the role of geometry on processes such as bone healing and remodelling (See also the groups of Wolfgang Wagermaier and Richard Weinkamer).

Related References:

  • Rumpler, M., et al. (2008). The effect of geometry on three-dimensional tissue growth. Journal of The Royal Society, Interface, 5(27), 1173–1180.
  • Dunlop, J. W. C., et al. (2010). A theoretical model for tissue growth in confined geometries. Journal of the Mechanics and Physics of Solids, 58(8), 1073–1087.
  • Bidan C. M. et al. (2012). How Linear Tension Converts to Curvature: Geometric Control of Bone Tissue Growth . PLoS ONE 7(5), e36336, doi:10.1371/journal.pone.0036336
  • Bidan C.M. et al. (2013). Geometry as a factor for tissue growth: Towards shape optimization of tissue engineering scaffolds. Advanced HealthCare Materials 2, 186-194.
  • Gamsjaeger, E., et al. (2013) The role of surface stress on the kinetics of tissue growth in confined geometries. Acta Biomaterialia 9, 5531-5543.
  • Bidan, C, M., et al, (2013) A three dimensional model for tissue deposition on complex surfaces, Computer Methods in Biomechanics and Biomedical Engineering, 16, 1056-1070.
  • Fischer, F. D., et al. (2015) Tissue growth controlled by geometric boundary conditions: a simple model recapitulating aspects of callus formation and bone healing, Journal of the Royal Society Interface, 12, 20150108.
  • Herklotz, M., et al, (2015), Availability of extracellular matrix biopolymers determines space-filling growth of human mesenchymal stem cells in vitro, Biomaterials, 60, 121-129.
  • Bidan, C. M., et al, (2016), Gradual conversion of cellular stress patterns into pre-stressed matrix architecture during in vitro tissue growth. Journal of the Royal Society Interface, 2016. 13: 20160136
  • Werner, M., et al, (2017), Surface Curvature Differentially Regulates Stem Cell Migration and Differentiation via Altered Attachment Morphology and Nuclear Deformation, Advanced Science, 2017, 4, 1600347.
  • Ehrig, S., et al (2017), Curvature controlled defect dynamics in active systems, accepted in Physical Review E
Web-View
Print Page
Open in new window
Estimated DIN-A4 page-width
Go to Editor View