Forschung
Protein Synthesis by Ribosomes
The synthesis of proteins is a fundamental task of all living cells because almost every cellular process is governed by proteins. Every protein consists of at least one chain of amino acids. The concatenation of individual amino acids into peptide chains is achieved by molecular machines called ribosomes. To synthesize a protein, a ribosome uses the genetic information stored in the corresponding messenger RNA (mRNA). A mRNA consists of a sequence of codons, each of which codes for a specific tRNA and, thus, for a specific amino acid. Each amino acid is carried by a transfer RNA (tRNA) molecule. An aminoacylated tRNA and an elongation factor EF-Tu form a ternary complex that reaches the ribosome by diffusive motion. The ribosome reads the mRNA codon by codon and takes up the corresponding ternary complexes, see Fig. 1. This process is called translation elongation.
Translation elongation is a nonuniform process with codon-specific elongation rates and error frequencies. This process has to meet conflicting requirements concerning speed and accuracy. On the one hand, protein synthesis must be fast enough to ensure doubling of protein mass within the time scale of cell division. On the other hand, translation must be very precise to avoid erroneous proteins that are often dysfunctional or even harmful to the cell. Therefore, perturbations that hamper or dysregulate protein synthesis can lead to all kinds of cellular defects and even to cell death, a well-known strategy to fight bacterial infections: Antibiotics kill microorganisms by blocking their protein synthesis. The speed and the accuracy of translation have direct influence, for example, on the folding dynamics of peptide chains and the functionality and abundance of the synthesized protein. It is therefore important to elucidate the underlying molecular mechanisms that influence the local and global speed and accuracy of translation. We developed and applied a theoretical framework for the process of protein synthesis to address this question.
Translation is a Stochastic Process
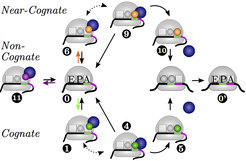
We describe translation as a Markov process to capture its stochastic nature, see Fig.2. Our theory takes major aspects of in vivo protein synthesis into account: We distinguish between non-cognate, near-cognate and cognate ternary complexes, which compete for binding to the ribosome in a concentration-dependent manner. The concentrations of free ternary complexes are calculated from the total tRNA concentrations by considering the details of a tRNA life cycle. These concentrations determine the codon-specific elongation rates and error frequencies. Like many other cellular processes, translation is a complex multistep process with numerous individual transitions of the molecules involved, see Figs. 1 and 2.
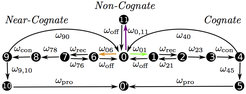
Fig. 2: Representation of translation as a codon-specific Markov process. For each codon c, the translation elongation cycle is represented by twelve states numbered from 0 to 11. The state (c|0) describes a ribosome with its A site at codon c and no initially bound tRNA. The states (c|1) - (c|5) represent the cognate branch for the decoding and full accommodation of a cognate tRNA. The states (c|6) - (c|10) belong to the near-cognate branch for the erroneous decoding of a near-cognate tRNA. The state (c|11) represents an initially bound non-cognate tRNA. An arrow from state i to state j indicates a transition with rate ωij. All rates of transitions between states are taken to be codon-independent, except for the binding rates of cognate, near-, and non-cognate ternary complexes (green, orange and purple arrows). State (c′|0′) is attained by the ribosome after translocation to the next codon c′.
The Kinetic Distance
Our theory incorporates experimental data on the rates of these transitions obtained by Marina V. Rodnina and her co-workers, our collaborators from the Max Planck Institute for Biophysical Chemistry (Göttingen). All transition rates were measured in vitro because so far it is not possible to determine these rates in vivo. To bridge the gap between in vitro measurements and in vivo translation, we developed a method to predict in vivo rates from their in vitro values. We introduced the kinetic distance, a new measure to quantitatively compare the kinetics of a process in different environments. We predicted the in vivo rates by a constrained minimization of this kinetic distance, see Fig. 3.
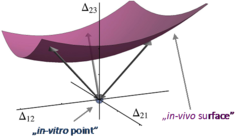
Fig. 3: Cartoon of a hypersurface in the multi-dimensional space of logarithmic differences ∆ij. The coordinates ∆ij represent the logarithmic differences ∆ij = ln(ωij/ω*ij) of the measured in vitro rates ωij and the predicted in vivo rates ω*ij. The origin of this space (light blue dot) corresponds to the in vitro system. The surface (purple) contains all points that correspond to a fixed measured in vivo value for the overall rate of protein synthesis. Each point on this surface has a certain “kinetic distance” that is equal to the Euclidean distance of this point from the origin, as indicated by the three double arrows. The point with the shortest kinetic distance determines the predicted in vivo rates.


